Деление столбиком: объясняем ребёнку сложную тему быстро и доступно

Многие наверняка помнят, как во время учёбы в начальной школе вечерами зубрили таблицу умножения, но упрямые цифры всё равно путались в голове. После освоения таблицы умножения младших школьников ждёт ещё одно испытание на прочность — деление в столбик; и простой зубрёжкой здесь не обойтись.

Мы расскажем, как объяснить это арифметическое действие вашему ребёнку простым языком, какие есть нюансы и лайфхаки, а также разберём примеры деления столбиком для третьего и четвёртого классов.

Содержание:

• Объясняем ребёнку правила деления
• Делим в столбик правильно
  • Деление на однозначные числа
  • Деление на двузначные числа
• Как делить числа с остатком?
• Деление дробей в столбик
• Примеры на деление уголком для начальной школы

Объясняем ребёнку правила деления

Fabio Principe/Shutterstock.com

Бывает, что беглой презентации новой темы во время школьного урока оказывается недостаточно для её понимания, и ваш третьеклассник идёт за разъяснениями к вам. Начните с объяснения ключевых понятий:

• деление — это действие, которое позволяет разбить какое-либо число на равные части. Иногда это возможно, иногда нет, и в последнем случае в результате деления образуется остаток. Приводите наглядные примеры: разделить шесть яблок на семью из трёх человек можно без труда, а вот четыре банана — уже сложнее: один банан останется;
• делимое — то число, которое нам необходимо разделить. В случае с яблоками — 6, а в примере с бананами — 4;
• делитель — число, на которое мы будем делить. В нашем случае — 3;
• частное — результат деления: каждому члену семьи достанется по два яблока и по одному банану.

Теперь переходим к основным правилам деления.

Правило 1

Деление — операция, противоположная умножению. Для деления на однозначные числа порой достаточно уверенного знания таблицы умножения: нужно просто «перевернуть» пример с делением и вспомнить нужную строчку из таблицы умножения.

Пусть ребёнок представит, что хочет угостить друзей конфетами, но не может разделить их поровну; всего в пакете 25 конфет, а ребят — пятеро:

25 ÷ 5 = ? → ? × 5 = 25 → Ответ: 5 конфет каждому.

Правило 2

Когда в качестве делимого выступает большее число, чем встречается в таблице умножения, для удобства мы разбиваем его на сумму из двух или трёх слагаемых и каждое делим по отдельности; сумма всех частных и будет ответом:

96 ÷ 4 = (40 + 40 + 16) ÷ 4 = (40 ÷ 4) + (40 ÷ 4) + (16 ÷ 4) = 10 + 10 + 4 = 24

Правило 3

При делении круглых чисел (оканчивающихся на 0) на другие круглые числа для удобства мы отбрасываем одинаковое количество нулей у делимого и делителя:

400 ÷ 80 = 40 ÷ 8 = 5

При делении круглого числа на однозначное операция выполняется без учёта нулей в конце делимого, а нули просто приписываются к полученному частному:

4200 ÷ 6 = ? → 42 ÷ 6 = 7 → 4200 ÷ 6 = 700

Существует также несколько базовых правил:

• делить на 0 нельзя;
• при делении на 1 делимое равно частному;
• если делимое и делитель одинаковые, частное равно 1;
• если делимое равно 0, то и частное будет равно 0.

Делим в столбик правильно

MNStudio/Shutterstock.com

Поняв основные принципы деления, ваш ребёнок без труда сможет применить их на практике. Но когда числа становятся длиннее, делить их в уме довольно сложно. Конечно, можно сделать это на калькуляторе. А если его нет под рукой? В этом случае применяют приём деления столбиком (его ещё называют деление уголком).

Деление на однозначные числа

Допустим, ребёнку нужно разделить 392 на 4. Разберём подробный алгоритм действий на этом примере.

1. Записываем пример таким образом, разделяя числа уголком: слева — делимое, справа — делитель, а внизу мы запишем частное:
   
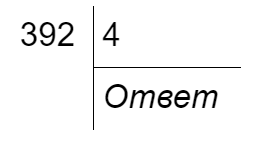
2. Ищем первое неполное делимое — то число, которое мы первым будем делить на 4. Для этого смотрим на делимое слева направо: число 3 меньше, чем 4, поэтому нам не подходит; значит, берём 39. Оно даст нам одну цифру в частном — отмечаем её точкой. Все оставшиеся после первого неполного делимого цифры также дают по одной цифре в частном — у нас это всего одна цифра 2, а значит, мы добавляем к частному всего одну точку.
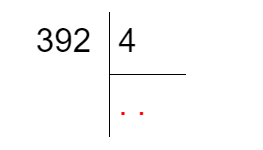
3. Посчитав количество цифр в частном, переходим к делению 39 на 4. Вспоминаем таблицу умножения на 4: ближайшее число, которое нам подходит — 36. Получаем первую цифру в частном: 36:4=9, и записываем её вместо первой точки в ответе. Записываем 36 под числом 39 и считаем остаток: 39–36=3. Если остаток оказался меньше делителя, наши подсчёты верны. Его записываем под чертой ниже:
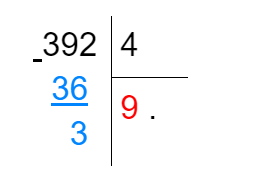
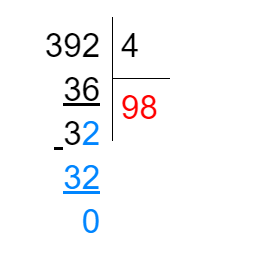
4. Теперь сносим оставшуюся в делимом цифру 2 к остатку и получаем число 32. Его нам снова необходимо разделить на 4. Вспомним таблицу умножения: 48=32. Значит, вторая цифра в ответе — 8. Записываем её на месте второй точки в частном. Итак, 3924=98. Мы поделили без остатка, поэтому под чертой подписываем 0.

Деление на двузначные числа

Итак, с делением на однозначное число проблем возникнуть не должно, если следовать алгоритму; но деление многозначных чисел на двузначное может вызвать сложности. Здесь выделить первое неполное делимое удаётся не всегда, и мы ищем частное к изначальному делимому методом подбора (по очереди умножаем делитель на 2, 3, 4 и т.д., пока не получим исходное делимое), а помогут нам некоторые хитрости, которыми делятся учителя математики:

• округляем делимое и делитель (цифры до 5 включительно округляем в меньшую сторону, от 6 — в большую), чтобы получить пробное частное;
• сразу умножаем делитель на 5, чтобы понять, в какую сторону нам двигаться дальше;
• делим разряды десятков из делимого на десятки из делителя.

Разберём эти приёмы в действии. Допустим, нам дан пример: 108÷18= ?

1. Запишем его столбиком и попробуем найти первое неполное делимое. 10 меньше 18, поэтому делить будем сразу всё трёхзначное делимое, а в ответе будет одна цифра:
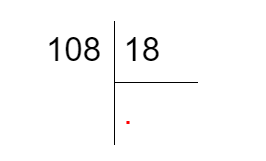
2. Округлим 108 до 110 и 18 до 20. Попробуем поделить 110 на 20: мы легко посчитаем, что 20×5=100, но 110>100, значит, нужно попробовать умножить 18 не на 5, а на 6:
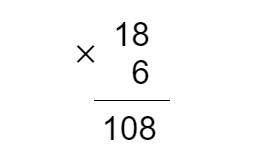
3. Итак, частное в нашем примере равно 6:

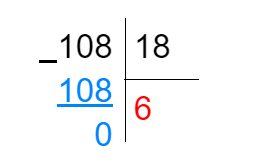
Проверим второй лайфхак. Допустим, нам необходимо разделить 90 на 15. Первое неполное делимое найти не получится — число 9 меньше 15, а значит, делить мы будем сразу 90:

1. Умножим 15 на 5 в столбик:
   
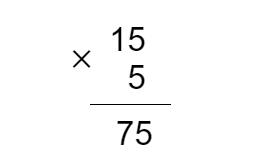
2. Этот результат меньше 90, зато мы знаем, в какую сторону двигаться: попробуем умножить 15 на 6 таким же образом и получим нужный нам ответ — 90. Значит, ответом на наш пример будет 6:
   

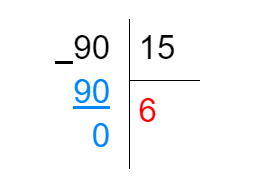
Опробуем третий совет: поделить разряды десятков в делимом и делителе. Это применимо к примерам, где делитель не начинается с 1.

1. Допустим, 180 необходимо разделить на 45. 18 на 4 не делится без остатка, но ближайшее к 18 число, которое делится на 4, это 16:
   16÷4=4
2. Попробуем умножить 45 на 4:
   
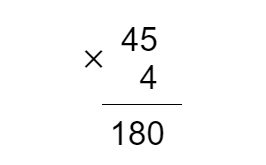
3. Итак, мы получили исходное делимое —180. Значит, ответ на наш пример — 4:
   

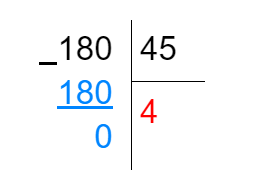
Получайте раз в месяц интересные материалы по обучению и воспитанию детей себе на почту. Подписывайтесь на нашу рассылку!

Как делить числа с остатком?

Prostock-studio/Shutterstock.com

Деление с остатком выполняется точно так же, как и любое другое деление; но в результате, помимо частного, мы получаем ещё и остаток, который всегда меньше делителя. Как объяснить это ребёнку? Приведите в пример любую покупку в магазине за наличные.

Допустим, ребёнок отправляется в пекарню за булочками; вы даёте ему 400 рублей, при этом одна булочка стоит 38 рублей. Вычислим, сколько булочек к завтраку и какую сдачу принесёт ваш ребёнок:

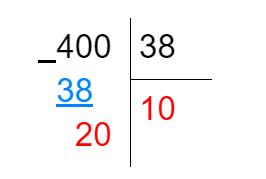
Первое неполное делимое — 40 — делится на 38 и даёт нам цифру 1 в частном; к оставшейся цифре 2 (40–38=2) сносим оставшийся от делимого 0. Но получившееся число 20 на 38 не делится нацело, поэтому в частном мы пишем 0, а 20 записываем в остаток:

400 ÷ 38 = 10 (ост. 20)

Таким образом, взяв с собой 400 рублей, ваш школьник принесёт домой 10 булочек по 38 рублей за каждую и 20 рублей сдачи.

Конечно, для двузначных чисел в пределах таблицы умножения применять деление в столбик не нужно: ответ можно найти путём подбора. Разберём пример:

53 ÷ 6 = ?

Здесь нужно вспомнить таблицу умножения на 6. Ближайшее к делимому 53 число, которое мы получаем при умножении 6 на 8 — 48. Далее необходимо вычислить остаток:

53 – 48 = 5

5<6, соответственно, мы правильно вычислили остаток (помним, что он не должен быть равен или больше делителя). Запишем ответ таким образом:

53 ÷ 6 = 8 (ост. 5)

Деление дробей в столбик

Iren_Geo/Shutterstock.com

В пятом классе школьники проходят деление столбиком десятичных дробей. Для того, чтобы объяснить ребёнку эту тему, следуйте алгоритму:

1. Делитель должен быть представлен в виде натурального числа. Для этого мы переносим запятые на одинаковое количество знаков вправо и в делимом, и в делителе.
2. Если делимое и так является натуральным числом, добавляем к нему необходимое количество нулей справа.
3. Далее делим в столбик так же, как любые натуральные числа.
4. Разделив целую часть делимого, мы ставим в частном запятую, после чего делим дробную часть.

Разберём этот алгоритм на примере:

2,28 ÷ 0,6 = ?

Переносим запятую:

2,28 ÷ 0,6 = 22,8 ÷ 6

Делим уголком:

Итак, 2,28 ÷ 0,6 = 3,8

Примеры на деление уголком для начальной школы

Проверьте, насколько хорошо ребёнок усвоил деление столбиком, предложив ему решить эти примеры:

⠀

Обучение делению в столбик — нелёгкая задача, особенно для тех родителей, которые далеки от точных наук и педагогики. Начинайте с простых примеров и постепенно наращивайте сложность, а главное — убедитесь в том, что ребёнок отлично знает таблицу умножения. Решайте как можно больше примеров, приводите примеры применения новых знаний в повседневной жизни и поддерживайте вашего школьника — тогда всё обязательно получится!

Источник фото обложки: fizkes/Shatterstock.com