Простая математика: объясняем школьнику, что такое целые числа
Для младших школьников, привыкших к тому, что числа используются для подсчёта или указания порядкового номера предметов, может стать настоящим открытием существование не только положительных, но и отрицательных чисел. В средней школе, когда ученики знакомятся с понятием целых чисел, у них могут возникнуть сложности в выполнении арифметических операций с ними.
В этом материале мы простыми словами объясняем, что такое целое число, чем оно отличается от натурального и какими свойствами обладает.
Содержание:
- Что такое целые числа?
- Все свойства целых чисел
- История изучения целых чисел
- Часто задаваемые вопросы по теме
Что такое целые числа?
Studio.G photography/Shutterstock.com
В начальной школе дети изучают понятие натуральных чисел — тех, которые мы используем для счёта. При помощи натуральных чисел ребёнок может сосчитать количество игрушек, конфет или любых других предметов. Но уже с пятого класса вводится определение целых чисел: это все натуральные числа, все противоположные натуральным (то есть со знаком «минус») и ноль. Иными словами, к целым числам относятся все положительные и отрицательные числа, а также ноль.
Целые числа необходимы для того, чтобы производить различные вычисления не только в положительную сторону, но и в отрицательную. С одними только натуральными числами произвести подобные вычисления было бы невозможно. Так, если из меньшего числа вычесть большее, получится отрицательное число.
Допустим, нам необходимо решить задачу: днём температура воздуха на улице была 3°, а ночью опустилась на 9°. Узнать, какая температура была ночью, нам поможет простой пример:
3–9 = –6
Отличительная особенность целых чисел — отсутствие дробной части или десятичных дробей. Значит, такие числа, как 314, –0,5 или 10,25 к целым не относятся.
Ряд целых чисел бесконечен, поэтому невозможно назвать наибольшее или наименьшее целое число. Множество целых чисел обозначается символом Z — по первой букве немецкого слова Zahlen, имеющего значение «числа». Это множество можно представить таким образом:
{∞… –4, –3, –2, –1, 0, 1, 2, 3, 4,…∞}
Какими бывают целые числа?
granata68/Shutterstock.com
Целые числа можно представить в виде числовой прямой: в центре неё расположен ноль, слева от него — числа со знаком «минус», а справа — натуральные числа.
Источник: arumath.ru
Таким образом, целые числа могут быть положительными и отрицательными:
- Положительные целые числа — это целые числа со знаком «плюс», или натуральные числа. Они всегда больше нуля: 21, 5, 156 и т. д.
- Отрицательные целые числа — это целые числа со знаком «минус», то есть они всегда меньше нуля: –7, –23, –752 и т. д. Все положительные, отрицательные числа и ноль образуют бесконечное множество целых чисел.
Что касается нуля, он не является ни положительным, ни отрицательным числом. Все положительные целые числа вместе с нулём называются неотрицательными, а все отрицательные целые числа вместе с нулём принято называть неположительными целыми числами.
Иными словами, неотрицательные целые числа — это те, которые больше либо равны нулю (100, 45, 0 и т. д.), а неположительные — те, которые меньше либо равны нулю (–17, 0, –129 и другие). Эти два термина используются для удобства и краткости формулировки условий задач. Допустим, нам необходимо сказать, что число b — это целое число, которое меньше или равно нулю, но проще определить его как целое неположительное число.
Отправляя ребёнка в школу, позаботьтесь об его безопасности. Установите приложение «Где мои дети», чтобы знать, где и когда он находится и что происходит вокруг него!
Все свойства целых чисел
Daniel Jedzura/Shutterstock.com
Целые числа обладают некоторыми важными свойствами, которые необходимо знать, чтобы выполнять арифметические действия с ними:
- замкнутость: выполняя сложение, вычитание или умножение целых чисел, в результате мы также получим целое число;
- переместительность: неважно, в каком порядке мы складываем или умножаем целые числа, ведь результат будет одинаковым (4+2=2+4). Вычитание и деление целых чисел этим свойством не обладают;
- распределительность: умножая целое число на сумму двух целых чисел, мы можем сначала умножить каждое слагаемое на это целое число, а затем сложить получившиеся произведения (3*(2+5)=3*2+3*5). Это же свойство применимо к операциям деления целых чисел: (6+8):2=6:2+8:2;
- разность знаков: умножая число со знаком «+» на число со знаком «–», мы всегда получаем произведение со знаком «–». Умножая числа с одинаковыми знаками, в результате получается положительное число (4*(–2)= –8; (–4)*(–2)=8);
- сочетательность: складывая и умножая три целых числа (или больше трёх), мы также можем по-разному группировать их без изменения конечного результата, например, 6*(4*2)=(6*4)*2;
- свойство нуля при сложении и вычитании: если мы прибавляем к целому числу ноль или вычитаем его, результат не меняется (5+0=5; 5–0=5);
- свойство нуля при умножении и делении: умножая любое число на ноль, в результате мы получаем ноль (7*0=0). Делить на ноль нельзя; но при делении нуля на любое число частное равно нулю (0:7=0);
- свойство противоположного элемента: сумма одинаковых чисел с разными знаками всегда равна нулю (9+(–9)=0);
- свойство единицы при умножении и делении: если любое целое число умножить или разделить на 1, результат останется неизменным.
Основные свойства сложения, вычитания, умножения и деления целых чисел с примерами мы представили в виде таблицы:
| Действие | Свойство | Пример |
| Сложение | Замкнутость | a+b∈Z |
| Переместительность | a+b=b+a | |
| Сочетательность | a+(b+c)=(a+b)+c | |
| Свойство нуля | a+0=a | |
| Свойство противоположного элемента | a+(–a)=0 | |
| Вычитание | Замкнутость | a–b∈Z |
| Свойство нуля | a–0=a | |
| Разность двух одинаковых целых чисел всегда равна нулю | a–a=0 | |
| Свойство вычитания целого числа из суммы двух чисел | (a+b)–c=a+(b–c)=(a–c)+b | |
| Свойство вычитания суммы из целого числа | a–(b+c)=a–b–c | |
| Умножение | Замкнутость | a*b∈Z |
| Переместительность | a*b=b*a | |
| Сочетательность | a*(b*c)=(a*b)*c | |
| Распределительность | a*(b+c)=a*b+a*c | |
| Свойство единицы | a*1=a | |
| Свойство нуля | a*0=0 | |
| Разность знаков | a*(–b)= –ab ⠀ (–a)*(–b)=ab |
|
| Деление | Распределительность | (a+b):c=a:c+b:c ⠀ (a–b):c=a:c–b:c |
| Разность знаков | a:(–b)= –c ⠀ (–a):(–b)=c |
|
| Любое целое число является делителем нуля | 0:a=0 | |
| Любое целое число можно разделить на 1 и на само себя | a:1=a ⠀ a:a=1 |
История изучения целых чисел
Djakandakandaduo/Shutterstock.com
Теория чисел, изучающая свойства целых чисел, уходит корнями в древние времена. Более шести тысяч лет назад натуральные числа начали использовать для подсчёта домашнего скота, мешков с зерном и других осязаемых объектов.
Дальнейшее развитие теория чисел получила только во втором веке до нашей эры, когда появились отрицательные числа: в Древнем Китае их использовали для обозначения суммы долга. При этом в Европе отрицательные числа стали использовать лишь в средние века. Долгое время учёные не могли прийти к единому мнению относительно использования и свойств таких чисел, и только в XIX веке окончательно сформировалась теория отрицательных чисел.
Прототипами цифр являлись зарубки на костях и кусках дерева, а впоследствии черточки. Источник: abakus-center.ru
Число 0 также прошло свою собственную непростую историю становления: о его существовании знали вавилонские учёные ещё в III веке до нашей эры, а также племена майя. Но в те времена учёные не рассматривали ноль как число, а обозначали специальными знаками: у вавилонян — двумя стрелами, поставленным наискось, а у майя — пробелом. Современное обозначение нуля появилось у индийцев в V веке.
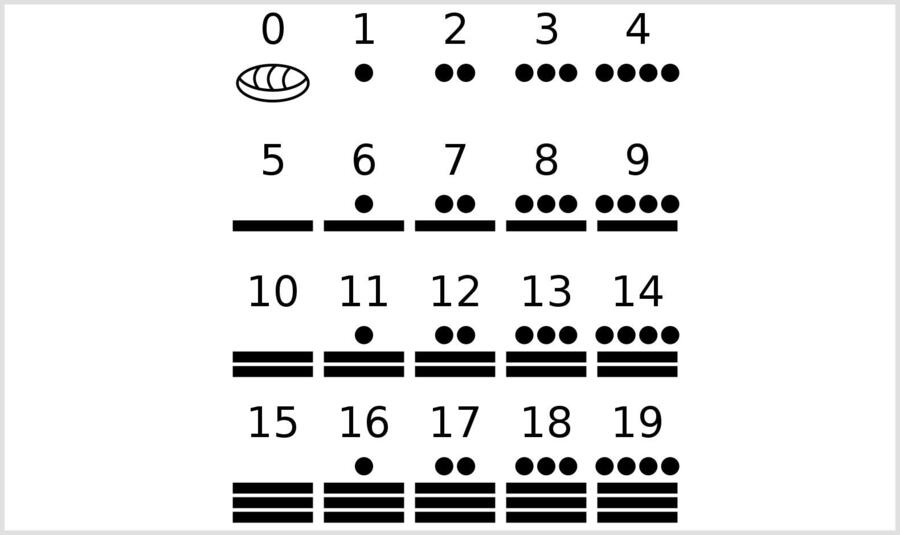
Двадцатеричная система счисления индейцев племени Майя. Источник: abakus-center.ru
Сегодня сложно представить, как можно производить какие-либо арифметические действия без отрицательных чисел или, например, нуля. Целые числа используются в самых разных областях: математике, физике, информатике, экономике и не только. В повседневной жизни также было бы непросто обойтись без отрицательных и положительных чисел, поэтому важно помочь ребёнку разобраться в этой новой и непростой для него теме.
Часто задаваемые вопросы по теме
Проверьте, насколько хорошо ваш школьник разобрался в материале, задав ему вопросы из этого раздела.
Что такое целые числа простыми словами?
Целые числа — это положительные числа, отрицательные и ноль.
Как выглядят целые числа?
Целые числа включают в себя натуральные числа (1, 2, 3, 4,…) и им противоположные (–1, –2, –3, –4,…), а также ноль, но у них не может быть дробной части. Так, числа 514, –2,25 или, например, 0,175 целыми не являются.
В чём разница между натуральным и целым числом?
Натуральные числа используются для подсчёта материальных объектов — это положительные числа от единицы до бесконечности. Целые числа — расширение множества натуральных чисел, так как включают в себя ещё и отрицательные числа, и ноль. То есть любое натуральное число является целым, но не любое целое число относится к натуральным.
И целые, и натуральные числа входят во множество рациональных чисел, которое включает в себя ещё и обыкновенные дроби.
Ноль — это целое число или нет?
Да, ноль является целым числом, но не является натуральным.
Источник фото обложки: L Julia/Shutterstock.com
Проверьте электронный ящик
